Puzzle of the Week #8

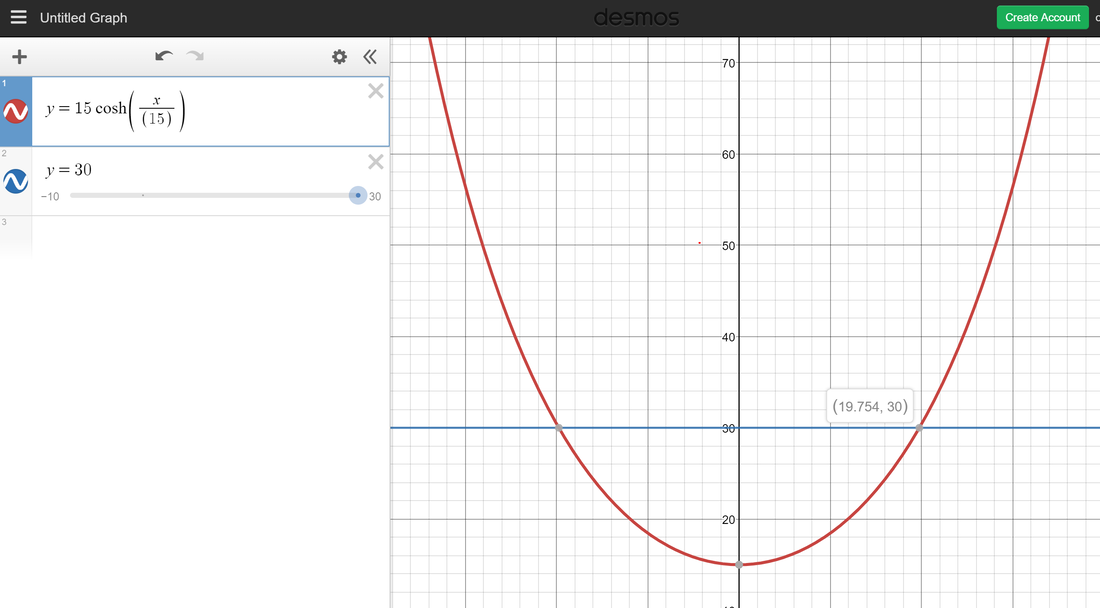
by Andrew Wu '19

To all who’ve labored over, laughed at, scoffed, overpassed, enjoyed, hated, or contributed to the seven Puzzles of the Week that have hitherto defined my Puzzle canon--

It is with a keen solicitude and with careful consideration that I have decided to lay down the vaunted mantle of “Puzzle Writer,” and retire to the more subdued cloister of “Puzzle Curator.” Whilst I shall still edit puzzles and find worthy authors of them, no longer (at least for the most part) shall I play an active role in their creation. Instead, this charge is conferred upon Andrew Wu ‘19, and possibly a rotating weekly syndicate of puzzlers as well, for whom I have the greatest expectations and in whom the highest confidence. While some details are still to be ironed out, please send responses to this week’s puzzle to Andrew Wu.

Curate ut valeatis,

NM ‘20


There were no successful solutions to either part of last week’s puzzle (however, there were some discrepancies and changes that likely could have precluded correct solutions—as Mr. Rick DuPuy pointed out, the lack of a k-term in the equation lent a myriad of uncertainty to the problem; I ought to have indicated that k should be assumed to be 0).

Answer to and commentary on Puzzle #7:
    Classification: Hard. For the main part of the puzzle, the temptation was to plug and chug with the formulae given, perhaps attempting to use calculus to factor in the length of the rope. However, one was required to realize that the required rope length, 50 feet, could never possibly reach 3 feet off the ground, given 30-foot poles; the rope would only reach 5 feet off the ground, even if the two poles were overlapping (30 – [50/2] = 5). Hence, there was no possible solution to the main problem. As for the bonus, it was a relatively simple calculation, because rope length was unlimited (and hence no calculus or catenary–distorting operations were necessary). I shall use a graph to illustrate it best (via Desmos.com):

As can be seen, for pole height 30 and catenary where a = 15, the absolute value of both x-terms is 19.754.



Puzzle #8
Andrew Wu (send responses to [email protected])

This Week’s Puzzle: This position was achieved through a series of legal chess moves. Find who played last (white/black).